فيزياء النسبية – الحلقة الأولى
مفهوم النسبية
قصة النسبية تبدأ من راكب يجلس في سيارة متحركة أو قطار وينظر إلى الرصيف. هو يرى نفسه جالسا ساكنا هادئاً في السيارة، بينما يرى الرصيف يمضي أمامه بسرعة إلى الخلف. والسؤال المهم: من الذي يتحرك منهما؟ والجواب هو أن السيارة والراكب يتحركان للأمام بالنسبة للرصيف، بينما الرصيف يتحرك للخلف بالنسبة إلى السيارة والراكب.
كلمة بالنسبة تأتي من السؤال من الذي يراقب ماذا. فالمراقب هو عنصر ضروري في نظرية النسبية الخاصة. ومن المهم جدا تحديد أين يوجد هذا المراقب قبل تحديد من الذي يتحرك وبأية سرعة.
بدأ الحديث عن النسبية قديما، لكن لعلنا نبدأ من غاليليو غاليلي. الذي وضع معادلات تصف هذه النسبية بين المراقب والمرصود. وكانت كلمة السر في هذه المعادلات هي الحركة بسرعة ثابتة. أي تجنب التعامل مع أي نوع من التسارع. والسبب في ذلك أنك عندما تتحرك بسرعة ثابتة، ( أو بعبارة أخرى تركب قطارا يتحرك بسرعة ثابتة مثلا) فلن يكون بمقدورك ان تدرك ان كان القطار متحركا ما لم تنظر من النافذة لترى حركة الرصيف أو السهل او الغابة حول القطار.
وبذلك يمكنك أن تقول أن سرعة القطار تساوي سرعة الرصيف مقدارا وتعاكسها اتجاها. فإذا سار أحد الركاب للأمام داخل القطار فهو بالتأكيد سيصل المحطة القادمة ‘‘أسرع‘‘ من الراكب الجالس في مقعده، وهذا ما يعرف بجمع السرع، حيث نجمع سرعة القطار مع سرعة المشي للراكب الماشي، بينما تبقى سرعة القطار فقط للراكب الجالس.
ولنأخذ حالة أعم من هذه ليكون بإمكاننا تطبيق مفهوم النسبية دون قيود. خذ حالة فيها سفينتان عملاقتان تمخران عباب المحيط، تسير إحداهما أسرع من الأخرى، لكنهما تسلكان مسارين متوازيين. على كل من هاتين السفينتين شخص يسير على سطح السفينة (بموازاة خط سيرها)، ويراقب أحد الشخصين حركة الآخر. لدينا السرعة النسبية بين السفينتين ولنسمها v (وهي الفرق بين سرعتي السفينتين، أي: v2 – v1). ولدينا الشخص الأول (ولنسمه المراقِب) يقف ساكنا على جانب سفينته يمسك بالحاجز ويراقب الآخر. أما الشخص الآخر (ولنسمه المراقَب أو المرصود) فيسير على سطح السفينة للأمام (أي بنفس اتجاه سير السفينة) ولتكن سرعته ‘u. وللتوضيح دعنا نتفق أن كل الكميات التي تخص المرصود نعطيها “فتحة” للتمييز. الآن كيف يقيس المراقب سرعة المرصود؟
بالنسبة للمراقب، يتحرك المرصود بسرعة ‘u فوق سطح سفينة تسير بسرعة وإذن فمن المنطقي أن سرعة المرصود تركب على سرعة السفينة فتصبح سرعة المرصود (كما يراها المراقب) هي: u= u’ + v ، وسميناها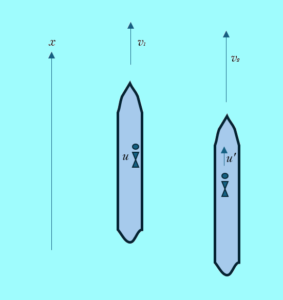
u بدون فتحة لأنها تخص قياس المراقب.
بينما لو كان المراقب هو الذي يتحرك للأمام والمرصود ساكن، وأردنا أن نرى كيف يقيس المرصود سرعة المراقب فسوف نرى أن سفينة المراقب ترجع للخلف بسرعة v (بالنسبة للمرصود) وبالتالي فإن تقدم المراقب للأمام يقلل منه ‘‘رجوع‘‘ سفينته للخلف وبالتالي فالمرصود يقيس سرعة المراقب لتكون: u’= u – v .
ومن هنا نقر أول معادلة من معادلات نسبية جاليليو بين سرعة المراقِب ux، وسرعة المرصود ‘ux، (حيث يأتي الترميز بدلالة x للتذكير أن الحركة هي في اتجاه محور x فقط)، والتي يمكن إدراجها كما يلي:
لاحظ هنا أن المراقب يوجد في إطار S ويمكن أن يتحرك داخله بسرعة u ، بينما المرصود يوجد في إطار ‘S ويمكن أن يتحرك داخله بسرعة ‘u. لكن الإطارين (السفينتين) يتحركان نسبة لبعضهما بسرعة v.
ولو أخذنا تطبيقات رقمية فستكون كما يلي:
إذا كانت السفينة اليسرى تتحرك للأمام بسرعة 5 م/ث واليمنى تتحرك للأمام بسرعة 8 م/ث فإن السرعة النسبية بين السفينتين (سرعة الأسرع نسبة للأبطأ) هي 8 – 5 = 3 م/ث. ماذا يعني ذلك. يعني أن السفينة اليسرى ترى نفسها ساكنة بينما اليسرى تسير للأمام بسرعة 3 م/ ث. أما السفينة اليمنى فترى نفسها ساكنة وترى اليسرى ترجع للوراء بسرعة 3 م/ث (يمكن أن نعتبرها بسرعة -3 م/ث)
الآن إذا سار المرصود على سطح سفينته (اليمنى) للأمام بسرعة 2 م/ث، فإن المراقب (الساكن) على السفينة اليسرى سوف يقيس سرعة المرصود حسب المعادلة أعلاه فتكون سرعة المرصود:
u= u’ + v = 2 + 3 = 5 m/s
أما إذا بدلنا الأدوار فسار المراقب على سطح سفينته (اليسرى) للأمام بسرعة 1 م/ث، فإن المرصود (الساكن الآن) على السفينة اليمنى سوف يقيس سرعة المراقب حسب المعادلة أعلاه فتكون سرعة المراقب:
u’= u – v = 1 – 3 = -2 m/s
يعني سيرى أن المراقب (بالنسبة له) يرجع للخلف بسرعة -2 م /ث.
كذلك تكون صياغة معادلة الموضع في كل من الاتجاهات الثلاثة x, y, z ، حيث يمكن التعبير عنها كما يلي:
هذه المعادلات تعطي الكميات التي تحمل فتحة كما هي للمرصود والتي لا تحمل فتحة هي للمراقب.
مثال:
ما هي الإزاحة x التي يقطعها المرصود على سطح سفينته خلال ثلاث ثوان من السير؟
الجواب:
x’ = u’t = 2 * 3 = 6 m
بينما تكون إزاحة المرصود التي يقيسها المراقب من سفينته هي:
x = x’ + vt = 6 + 3 * 3 = 6 + 9 = 15 m.
فبالنسبة للمراقب تحرك المرصود للامام مسافة 15 مترا، والسبب ان موضع المرصود يتغير بسيره الذاتي وكذلك بسير السفينة التي يوجد عليها. ولو ان المرصود بقي ساكنا، لرآه المراقب قد تحرك (مع سفينته) مسافة 3 * 3 = 9 امتار.
***
في الحلقة الثانية سنتناول الديناميكا الكلاسيكية، وهي تتضمن معالجات للأنظمة باستخدام معادلات الحركة وقوانين نيوتن في نطاق السرعات المألوفة لنا في حياتنا اليومية.